道德风险习题

离散模型

※第一期，某店主打算雇佣一个雇员，开出工资 $w$ ；第二期，雇员选择是否接受工作，如果不接受则博弈结束，假设店员接受工作的机会成本为 0；第三期，雇员选择努力水平 $e \in {e_{1}, e_{2}, e_{3}}$ ，付出的努力成本和获得产出 $π \in {π_{H} = 10, π_{L} = 0}$ 的概率如下：

g (e_{i}) = {\begin{cases} \frac{5}{3} & , i = 1 \\ \frac{8}{5} & , i = 2 \\ \frac{4}{3} & , i = 3 \end{cases} P (π_{H} ∣ e_{i}) = {\begin{cases} \frac{2}{3} & , i = 1 \\ \frac{1}{2} & , i = 2 \\ \frac{1}{3} & , i = 3 \end{cases}

第四期，店主获得收益 $v = π - w$ ，雇员获得收益 $u = \sqrt{w} - g (e)$

如果努力水平是可观测的，雇员会选择什么努力水平
如果努力水平是不可观测的，证明 $e_{2}$ 是不可实施的
如果努力水平是不可观测的，最优合约是什么？

【1】

\begin{aligned} max_{w, e} & v = π - w \\ s.t. & u = \sqrt{w} - g (e) \geq 0 \end{aligned}

店主总可以降低 $w$ 使得约束为紧，即令

w (e_{i}) = {\begin{cases} \frac{25}{9} & , i = 1 \\ \frac{64}{25} & , i = 2 \\ \frac{16}{9} & , i = 3 \end{cases} ⟹ v_{i} = {\begin{cases} \frac{2}{3} \times 10 - \frac{25}{9} = \frac{35}{9} & , i = 1 \\ \frac{1}{2} \times 10 - \frac{64}{25} = \frac{61}{25} & , i = 2 \\ \frac{1}{3} \times 10 - \frac{16}{9} = \frac{14}{9} & , i = 3 \end{cases}

要使得 $v^{*} = max {v_{i}}$ ，则 $w^{*} = \frac{25}{9}, e^{*} = e_{1}$

【2】
店主依据产出制定工资 $w \in {w_{H}, w_{L}}$ ，雇员实施 $e_{2}$ 需要满足

\begin{aligned} \frac{1}{2} \sqrt{w_{H}} + \frac{1}{2} \sqrt{w_{L}} - \frac{8}{5} & \geq \frac{2}{3} \sqrt{w_{H}} + \frac{1}{3} \sqrt{w_{L}} - \frac{5}{3} \\ \frac{1}{2} \sqrt{w_{H}} + \frac{1}{2} \sqrt{w_{L}} - \frac{8}{5} & \geq \frac{1}{3} \sqrt{w_{H}} + \frac{2}{3} \sqrt{w_{L}} - \frac{4}{3} \end{aligned}

即激励相容约束。化简为

\begin{aligned} \sqrt{w_{H}} - \sqrt{w_{L}} & \leq \frac{2}{5} \\ \sqrt{w_{H}} - \sqrt{w_{L}} & \geq \frac{8}{5} \end{aligned}

两式矛盾，故 $e_{2}$ 是不可实施的。

【3】
店主依据产出制定工资 $w \in {w_{H}, w_{L}}$ ，店主需要激励 $e_{1}$

\begin{aligned} max_{w, e} & v = \frac{2}{3} \times (10 - w_{H}) + \frac{1}{3} \times (0 - w_{L}) \\ s.t. & \frac{2}{3} \times \sqrt{w_{H}} + \frac{1}{3} \times \sqrt{w_{L}} - \frac{5}{3} \geq 0 (IR) \\ \frac{2}{3} \times \sqrt{w_{H}} + \frac{1}{3} \times \sqrt{w_{L}} - \frac{5}{3} \geq \frac{1}{2} \sqrt{w_{H}} + \frac{1}{2} \sqrt{w_{L}} - \frac{8}{5} (IC1) \\ \frac{2}{3} \times \sqrt{w_{H}} + \frac{1}{3} \times \sqrt{w_{L}} - \frac{5}{3} \geq \frac{1}{3} \sqrt{w_{H}} + \frac{2}{3} \sqrt{w_{L}} - \frac{4}{3} (IC2) \end{aligned}

其中 IC 1 和 IC 2 可化简为

{\begin{cases} \sqrt{w_{H}} - \sqrt{w_{L}} \geq 10 - 9 \frac{3}{5} & (IC1) \\ \sqrt{w_{H}} - \sqrt{w_{L}} \geq 1 & (IC2) \end{cases}

因此 IC 1 是可忽略的。

最优化问题等价于

\begin{array}{r} \begin{aligned} min_{w} & 2 w_{H} + w_{L} \\ s.t. & 2 \sqrt{w_{H}} + \sqrt{w_{L}} \geq 5 \\ \sqrt{w_{H}} - \sqrt{w_{L}} \geq 1 \end{aligned} \end{array}

在坐标系 $(\sqrt{w_{L}}, \sqrt{w_{H}})$ 中，这相当于问在约束下何时椭圆函数值最小

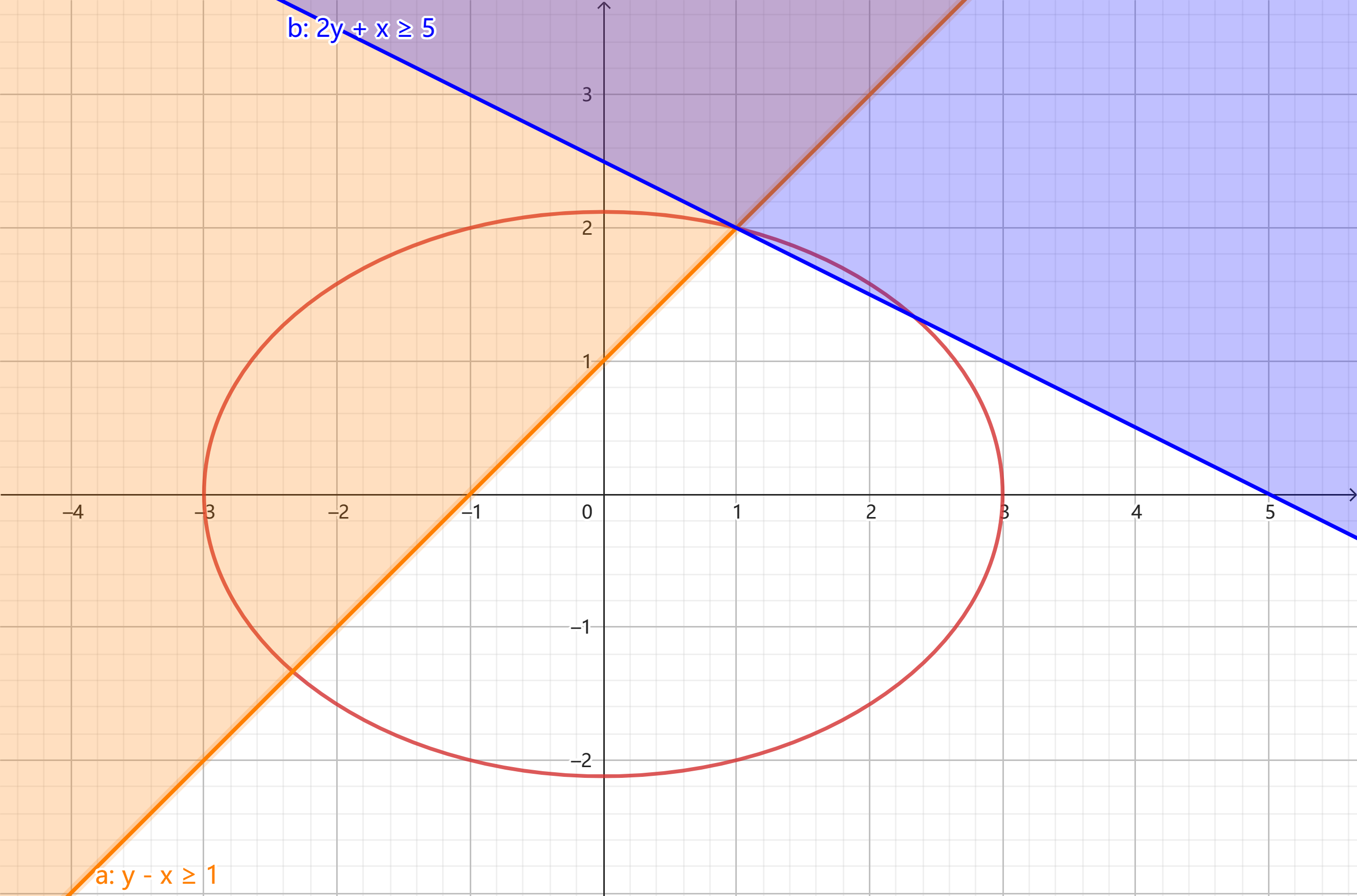
显然，最优点在两个约束线交点处取得

{\begin{cases} 2 \sqrt{w_{H}} + \sqrt{w_{L}} = 5 \\ \sqrt{w_{H}} - \sqrt{w_{L}} = 1 \end{cases} ⟹ w_{H} = 4, w_{L} = 1

此时 $e^{*} = e_{1}, v^{*} = \frac{11}{3}$

连续模型

※假设一个店主要雇佣一个店员， $R$ 为店主获得的利润， $e$ 为店员的努力程度，满足

R (e) = 4 e + η where η \in N (0, σ^{2})

店员的成本函数为 $c (e) = e^{2}$ ，工资合约形式为 $w = A + B \cdot R (e)$ ，机会成本为 1，假设努力程度是不可观测的，求店主的最优工资合约。

\begin{aligned} max_{A, B} & 4 e + E [η] - A - B \cdot (4 e + E [η]) \\ s.t. & A + B \cdot (4 e + E [η]) - e^{2} \geq 1 \\ e = \underset{\hat{e}}{\arg max} A + B \cdot (4 \hat{e} + E [η]) - {\hat{e}}^{2} \end{aligned}

激励相容约束解得（抛物线性质）

e = 2 B

店主可以降低 $A$ 使得参与约束取等号

A + 4 B^{2} = 1

约束条件代入目标函数

8 B - 4 B^{2} - 1 ⟹ B^{*} = 1, A^{*} = - 3, e^{*} = 2

最优工资合约为

w = - 3 + R

SPNE 为

{w = 5 + η, e = 2}

这里店主和店员都是风险中性，产生的合约是店主获得固定租金 3，店员承担风险。

※某企业家有个投资项目，初始投资额为 6，若成功则收入为 48，若失败则收入为 0。项目成功的概率等于企业家的努力水平 $e \in [0, 1]$ ，努力成本为 $40 e^{2}$ ，努力水平是私人信息。假设企业没有资金，所有人都是风险中性，不存在贴现。

如果企业家使用自有资金投资，他会选择什么努力水平，净利润多少？
如果企业家没有资金，需要向银行借款进行初始投资。博弈时序如下：第一期银行向企业家提出借款合约，规定项目成功还款为 $D$ ，项目失败还款为 0；第二期企业家决定是否接受合约，如果拒绝则博弈结束；第三期企业家选择努力水平；第四期各方收益实现。此时企业家会选择什么努力水平，净利润多少？银行规定的还款 $D$ 是多少？

【1】

max_{e} π = 48 e - 40 e^{2} - 6

根据抛物线性质， $e^{*} = \frac{3}{5}, π^{*} = \frac{42}{5}$

【2】

\begin{aligned} max_{e, D} & v = e D - 6 \\ s.t. & e (48 - D) - 40 e^{2} \geq 0 (IR) \\ e = \arg max_{\hat{e}} \hat{e} (48 - D) - 40 {\hat{e}}^{2} (IC) \end{aligned}

银行总可以提高 $D$ 提高收益使得 IR 是紧约束，与 IC 都可得 $e = \frac{48 - D}{80}$

代入目标函数可得

max_{D} v = \frac{(48 - D) D}{80} - 6

根据抛物线的性质， $D^{*} = 24, e^{*} = \frac{3}{10}, π^{*} = \frac{18}{5}$